FRACTALES Y AUTÓMATAS CELULARES

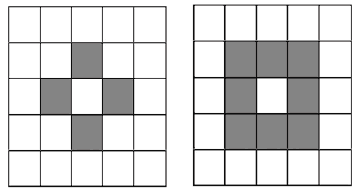
Un autómata celular (A.C.) es un modelo matemático para un sistema dinámico que consiste en una rejilla formada por celdas llamadas “células” que pueden cambiar de estado o no, según leyes que evalúan los estados de las células vecinas. Los autómatas celulares fueron inventados a fines de los cuarenta por Stanislaw Ulam (1909-1984) y John von Neumann (1903-1957)
John von Neumann		Stanislaw Ulam

Existen muchas variaciones de AC. Los más simples se desarrollan en una dimensión. Un ejemplo podría ser una fila de células cada una evaluando constantemente a sus dos vecinas para decidir de qué color teñirse. La pigmentación del caracol, por ejemplo, puede considerarse como unión de autómatas celulares como el descrito en el párrafo anterior.
Los AC pueden ser construídos en dos dimensiones.En los de trama cuadriculada, cada célula se puede considerar como viviendo en un vecindario de cinco o nueve células, ella misma incluida.

También puede construirse AC usando células triangulares o hexagonales:

En la imagen inferior podemos ver AC de tres dimensiones:

Veamos un video donde un autómata celular simula una distribución de temperatura.Cada célula se vuelve más caliente o más fría según la influencia de sus vecinas.

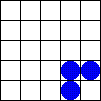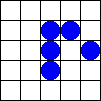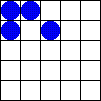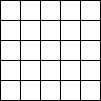
Uno de los AC mas conocidos es el Juego de la vida, creado por John Horton Conway en 1970. El juego consiste en una cuadrícula donde se coloca al inicio un patrón de células «vivas» o «muertas». La vecindad para cada célula son los ocho celdas que la rodean. De manera repetida, se aplican simultáneamente sobre todas las células de la cuadrícula las siguientes 3 reglas:
Nacimiento: se reemplaza una célula muerta por una viva si dicha célula tiene exactamente 3 vecinos vivos. Muerte: se reemplaza una célula viva por una muerta si dicha célula no tiene más de 1 vecino vivo (muerte por aislamiento) o si tiene más de 3 vecinos vivos (muerte por sobrepoblación). Supervivencia: una célula viva permanecerá en ese estado si tiene 2 o 3 vecinos vivos.
El Juego de la Vida tuvo mucha popularidad gracias a aparición de una nueva generación de computadores económicos en el mercado . Desde su publicación, el juego atrajo mucho interés debido a la gran variabilidad de la evolución de los patrones. El Juego de la vida denotaba un ejemplo de auto-replicación y auto-organización similar a los sistemas biológicos. Por esta razón los científicos estudiaron la implementación del juego, observando la forma en la que complejos patrones pueden surgir de la definición de una serie de reglas muy sencillas. En el vídeo siguiente podemos ver una demostración de este juego:

Relación de los autómatas celulares con los fractales
Centrándonos en el tema que nos ocupa, cabe decir que algunos fractales puedes ser generados usando autómatas celulares. Como ejemplo particular, en la imagen podemos ver al Triángulo de Sierpinski obtenido a través de uno de estos AC.
Por otra parte, algunos científicos han sugerido la posibilidad de generar fractales L-system equivalentes a autómatas celulares debido a la identificación de algunas similitudes entre ambos sistemas: • Los dos tienen información inicial que puede ser considerada como su estado de partida. — Para un sistema L, esta información incial es el axioma. — Para un autómata celular, el conjunto de todos los estados iniciales de sus autómatas• Los dos tienen componentes en los que se codifica la manera de cambiar del sistema. — En un sistema L, el conjunto de reglas de producción. — En un autómata celular, la función de transición de sus autómatas finitos. • Las dos arquitecturas generan el próximo estado aplicando su transformación a todos los componentes de la estructura en paralelo. — Los sistemas L cambian cada símbolo de la palabra transformada. — Los autómatas celulares cambian el estado de cada autómata de la rejilla.Estas similitudes sugieren la posibilidad de encontrar una convergencia entre autómatas celulares y sistemas L.